Data, Syntax and Semantics

A Guide for the Reader

The educational objectives of the book are as follows:

Educational Objectives

To study some theoretical concepts and results concerning abstract data types; programming language syntax; and programming language semantics.

To develop mathematical knowledge and skills in mathematically modelling computing systems.

To introduce some of the intellectual history, technical development, organisation and style of the scientific study of programming languages.

At the heart of the book is the idea that the theory presented is intended to answer some simple scientific questions about programming languages. A long list of scientific questions is given in Section 1.2. To answer these questions we must mathematically model data, syntax and semantics, and analyse the models in some mathematical depth. In addition to meeting the objectives above, we hope that our book will help the students learn early in their intellectual development the following:

Intellectual Experiences

That the mathematical theory gives interesting and definitive answers to essential questions about programming.

That the theory improves the capacity for practical problem solving.

That the answers to the scientific questions posed involve a wide range of technical material, that was invented and developed by many able people over most of the twentieth century, and has its roots in the nineteenth century.

That the theory contains technical ideas that may be expected to be useful for decades if not centuries.

That intellectual curiosity and the ability to satisfy it are ends in themselves.

It will be helpful to summarise the structure and contents of the book, part by part, to ease its use by the reader, whether student or teacher.

Subjects

Data, syntax and semantics are fundamental and ubiquitous in Computer Science. This book introduces these three subjects through the theoretical study of programming languages. The subjects are intimately connected, of course, and our aim is to integrate their study through the course of the whole book. However, we have found it natural and practical to divide the text into three rather obvious parts, namely on data, syntax and semantics. We begin with a general overview of the whole subject, and a short history of the development of imperative programming languages.

Part I is on data. It is an introduction to abstract data types. It is based on the algebraic theory of data and complements their widespread use in practice. We cover many examples of basic data types, and model the interfaces and implementations of arbitrary data types, and their axiomatic specifications. We focus on the data types of the natural numbers and real numbers, data in time and space, and terms.

Part II is on syntax. It introduces the problem of designing and specifying syntax using formal languages and grammars, and it develops a little of the theory of regular and context free grammars. Again, there are plenty of examples to motivate and illustrate the language definition methods and their mathematical theory. Our three main case studies are simple but influential: addresses, interface definition languages and imperative programming languages. We round off the topic by applying data type theory to abstract syntax and the definition of languages.

Part III is on semantics. It introduces some methods for defining the semantics of imperative programs using states and their transformation. It also deals with proving properties of programs using structural induction. We conclude with a study of compiler correctness. We define a simple virtual machine and compiler from an imperative language into its virtual assembler and prove by structural induction that it is correct.

In the book explanations are detailed and examples are abundant. There are plenty of exercises, both easy and hard, including some longer assignments.

The final chapter of each part contains advanced undergraduate material that brings together ideas and results from earlier chapters. Occasionally, sections in other chapters will also contain such advanced material. We will mark chapters and sections with advanced material using $$*$$.

Options

Rarely are the chapters of a scientific textbook read in order. Lecturers and students have their own ideas and needs that lead them to re-order, select or plunder the finely gauged writings of authors. This textbook presents a coherent and systematic account of the theory of programming languages, but it is flexible and can be used in several ways. We certainly hope the book will be plundered for its treasures.

The structure of the book is depicted in Figure 1, which describes the dependency of one chapter upon another. The chapters may be read in a number of different orders. For example, all of Part I can be read independently of Part II, but Chapter 16 of Part II depends on Chapters 3-6 of Part I.

The complete course can be given by reading all the chapters in order. As noted, it is easy to swap the order of Part I and Part II.

A concise course that covers the mathematical modelling of an imperative language with arbitrary data types, but without the advanced topics, can be based on this selection of chapters:

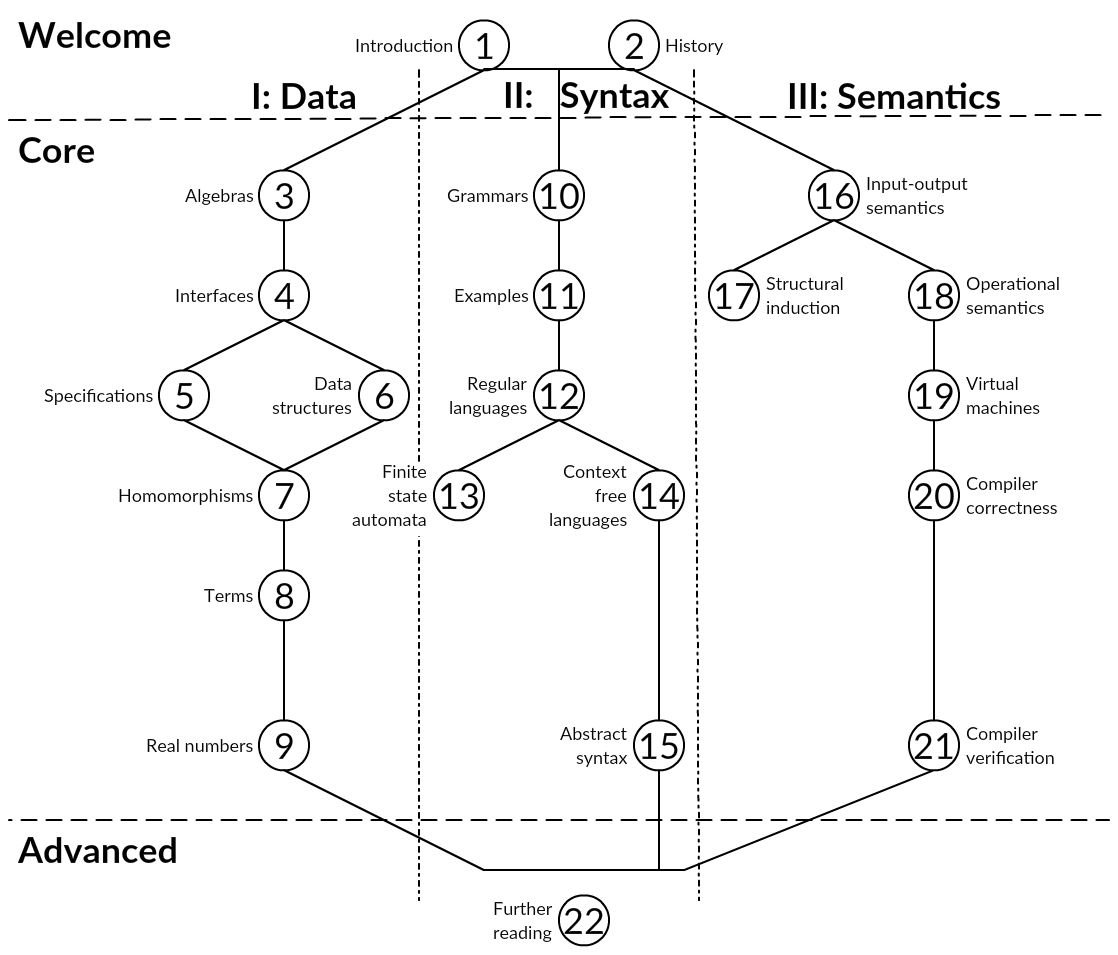Figure 1: Structure of the book

Data: Chapters 1, 3—7
Syntax: Chapters 10—14
Semantics: Chapters 16 and 17

Shorter and easier courses are also practical:

Data: Chapters 1, 3—6
Syntax: Chapter 10 and 11
Semantics: Chapters 16 and 18

A set of lectures on data types can be based on:

Data: Chapters 3—9
Syntax: Chapter 15
Semantics: Chapter 16 and 17

A set of lectures on syntax can be based on:

Data: Chapters 3—4
Syntax: Chapters 10—15

A set of lectures on hierarchical structure and correct compilation can be based on:

Syntax: Chapter 10 and 11.
Semantics: Chapter 16—17 and 19—21.

Prerequisites

Throughout, we assume that readers have a sound knowledge and experience of

programming with an imperative language;
sets, functions and relations;
number systems and induction;
propositional and predicate logic; and
axioms and deduction.

However, our chapters provide plenty of reminders and opportunities for revising these essential subjects. Students who take the trouble to revise these topics thoroughly, here at the start, or even as they are needed in the book, will progress smoothly and speedily. Occasionally, for certain topics, we will use or mention some more advanced concepts and results from abstract algebra, computability theory and logic. Hopefully, these ideas will be clear and only add to the richness of the subject.

Notation

We will follow the discipline of mathematical writing, adopting its standard notations, forms of expression and practices. It should be an objective for the student of Computer Science to master the elements of mathematical notation and style.

Notation in Computer Science is very important and always complicated by the need for concepts to have three forms of notation:

Mathematical Notation: is designed to facilitate mathematical expression and analysis of general ideas and small illustrative examples;
Descriptive Notation: is designed to facilitate reading and comprehension of large examples and case studies; and
Machine Notation: is designed to facilitate processing by machine.

Several of our key concepts (algebras, grammars, programs, etc.) will be equipped with two standard notations aimed at the Mathematical Notation and Descriptive Notation.

Exercises and Assignments

At the end of each chapter there is a set of problems and assignments designed to improve and test the student's understanding and technique. Some have been suggested by students. The problems illustrate, complete, explore, or generalise the concepts, examples and results of the chapter.

Revision

We end this Guide with an assignment that invites students to revise the prerequisites and with a piece of advice: do this assignment, and do it well.

Prepare a concise list of concepts, notations and results that you believe are the basics of the five topics mentioned in the Prerequisites. Add to this list as you study the following chapters. Here is a start.

Programming

variable
expression
assignment
sequencing
conditional branching
iteration
procedure
array, list, queue, stack
⋮

Sets

$$\emptyset$$	$$A \not= \emptyset$$
$$x \in A$$	$$x \notin A$$
$$A \subseteq B$$	$$A \nsubseteq B$$
$$A \cup B$$	$$A \cap B$$
$$A$$ — $$B$$	$$P(A)$$
$$\mid A \mid $$

⋮

Functions

$$f : A \rightarrow B$$
$$g \circ f : A \rightarrow C$$ where $$f : A \rightarrow B$$ and $$g : B \rightarrow C$$.
$$f$$ is total.
$$f$$ is partial.
$$f$$ is injective, or one-to-one.
$$f$$ is surjective, or onto.
$$f$$ is bijective, or a one-to-one correspondence.
⋮

Relations

$$R \subset A \times B$$	$$xRy$$
$$\equiv$$ equivalence relation	$$[a]$$ equivalence class
$$\leq$$ partial order
$$\leq$$ total order

⋮

Number Systems

$$\mathbb{N}$$: natural numbers
$$\mathbb{Z}$$: integers
$$\mathbb{Q}$$: rational numbers
$$\mathbb{R}$$: real numbers

Logic

$$ p \wedge q $$
$$ p \vee q $$
$$ p \Rightarrow q $$
$$ \neg p $$
$$ \forall x : R(x) $$
$$ \exists x : R(x) $$
⋮

Axiomatic Theory

definition
axiom
postulate
law
lemma
theorem
corollary
proof
deduction
counter-example
conjecture
⋮